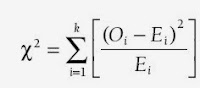Popper, a tábua de Galton e a experiência da dupla fenda: materiais e metodologia do projecto

Após a parte teórica do projecto (ver aqui e aqui), a parte prática do mesmo consistiu essencialmente na construção de duas tábuas de Galton, uma com todos os 'pregos' (dita normal) e a outra sem um dos 'pregos' - tal como indicado no texto de Sir Karl Popper que serviu de mote ao projecto. As fotografias abaixo ilustram o trabalho de carpintaria executado pelos alunos na construção das duas tábuas de Galton:

Para a construção das tábuas de Galton, os alunos do Clube usaram como esquema de trabalho a figura abaixo [inch (polegada), 1 in = 2,54 cm], devidamente reescalada para o diâmetro das esferas usadas no projecto, tendo utilizado os seguintes materiais:

1. 54 esferas metálicas de 1,5 cm Ø;
2. 1 paquímetro metálico, para a medição do diâmetro das esferas;
3. 2 bases de madeira contraplacada de dimensões 60 x 30 x 1 cm;
4. pinos de madeira de 1,5 cm e 1 cm Ø, correspondendo aos ditos 'pregos' das tábuas de Galton (ver fotografias acima);
5. pregos de cobre de 2 cm e 1,5 mm Ø e cola de madeira para fixar os pinos de madeira às tábuas de Galton [em vez de pregos, outra opção mais fácil de aplicar seria o uso de cola superforte];
6. ripas de madeira aplainada (com 4,4 cm de altura), para servirem de bordos às tábuas de Galton (ver fotografia abaixo); 
7. 4 divisores (em k-line e cartolina pretos), para dividirem a base das tábuas de Galton em 5 'caixas' de igual largura (ver fotografia abaixo);
8. 2 arquivadores de dossiês (1 para cada tábua), utilizados como suporte de inclinação das tábuas de Galton;
9. materiais vários de pintura e carpintaria para os acabamentos (spray de tinta preta, tintas várias, k-line preto, cola superforte, lixa, martelos, etc.)

Enquanto os alunos procederam à parte da carpintaria, os acabamentos finais ficaram sob responsabilidade do prof. coordenador, podendo ver-se, na figura ao lado, a tábua de Galton sem um dos 'pregos' finalizada. A localização do 'prego ausente' (assinalado a vermelho) resultou de um prego de cobre mal martelado que impossibilitou a colocação de um pino de madeira nesse local. A relação entre o diâmetro das esferas e o diâmetro dos pinos de madeira foi mantida muito próxima, dada a sua influência na largura das distribuições de probabilidade obtidas em tábuas de Galton, como se pode verificar no vídeo seguinte:

 

Mais detalhes sobre a construção de tábuas de Galton simples - com a habitual geometria triangular, que permite visualizar mais facilmente a relação da tábua de Galton com o triângulo de Pascal (ver aqui e aqui) - podem ser vistos no vídeo que se mostra a seguir:

 

 

Relativamente às tábuas construídas no Clube de Ciências, a fotografia abaixo mostra as duas lado a lado, bem como o grupo de alunos (Os Poppers) responsáveis pelo projecto.

Em termos metodológicos, e para além do óbvio trabalho de carpintaria, o projecto dividiu-se em três etapas, a saber:

1. construção da tábua de Galton sem um dos 'pregos' e obtenção da respectiva distribuição de frequências dos resultados, com a realização de 8 séries de quedas das 54 esferas metálicas a partir do topo da tábua;
2. construção da tábua de Galton com todos os 'pregos' (normal) e obtenção da respectiva distribuição de frequências dos resultados, repetindo o procedimento de queda das esferas referido no ponto anterior;
3. realização do teste do qui-quadrado para comparação das distribuições de frequências obtidas com as duas tábuas de Galton, tendo o valor da variável estatística (o qui-quadrado) sido calculado de acordo com a fórmula apresentada no post de 12 de Julho.

Os resultados do teste estatístico do qui-quadrado, bem como as conclusões do projecto serão apresentados no próximo post.

Popper, a tábua de Galton e a experiência da dupla fenda: o teste estatístico do qui-quadrado

No seguimento do post anterior, e de modo a poderem testar quão próximas (ou não) vão ser as distribuições das esferas nas duas tábuas de Galton, os alunos do grupo Os Poppers tiveram de aprender algumas noções sobre o teste estatístico do qui-quadrado, matéria dada na disciplina de Biologia do ensino secundário de países anglo-saxónicos como os EUA e Inglaterra, onde os alunos têm de aprender a testar predições quantitativas sobre sistemas biológicos.

De modo a manter tudo o mais simples possível, os alunos do Clube de Ciências aprenderam o teste do qui-quadrado a partir do livro Nuffield Science Calculations, dirigido a alunos ingleses dos 11-14 anos e 14-16 anos inscritos em cursos GCSE de Ciência.

O qui-quadrado é, então, uma variável estatística calculada a partir do somatório das diferenças entre os resultados observados, Oi, e os resultados esperados, Ei, de acordo com a seguinte fórmula:

onde i = 1, 2, ..., k é o n.º de divisões (ou classes ou 'caixas') pelas quais se distribuem os vários resultados.

 Comparando o valor calculado com certos valores críticos (que dependem do nível de probabilidade e dos chamados 'graus de liberdade') é possível determinar quão bem os resultados observados se aproximam dos esperados. A tabela abaixo apresenta vários desses valores críticos, para diferentes níveis de probabilidade (em %) e graus de liberdade (g.l.):

O exercício seguinte, retirado do livro supracitado, pode mostrar como se aplica o teste do qui-quadrado e qual o significado dos 'graus de liberdade'.
 
Considere-se uma experiência simples com 96 bichos-de-conta contidos numa caixa dividida em duas metades, estando a metade A às escuras e a metade B iluminada. Com todas as outras variáveis controladas, o n.º observado de bichos-de-conta em cada uma das metades foi:

Metade A (às escuras): 73 bichos-de-conta   ||   Metade B (iluminada): 23 bichos-de-conta

 

Serão estes resultados devidos ao acaso? Se não, que conclusões se podem retirar da experiência?
 
RESOLUÇÃO: 
 
Dados:
Oescuro = 73; Oiluminado = 23
Eescuro = 48; Eiluminado = 48 (admitindo que os bichos-de-conta se distribuíram aleatoriamente pelas duas metades da caixa)

Calculando o valor do qui-quadrado, obtém-se:

onde 10,83 é o valor crítico da tabela para 1 grau de liberdade e um nível de probabilidade de 0,1%. O 'grau de liberdade' é a resposta à pergunta: "Se o animal não fez esta escolha, quantas mais estavam disponíveis?". Neste caso, existia apenas mais uma escolha ou grau de liberdade. O valor 0,1% representa a probabilidade de os resultados obtidos se deverem ao acaso, pelo que, com um nível de confiança de 99,9%, podemos concluir que outra razão, para além do acaso, foi responsável pelos resultados da experiência, podendo-se considerar que os bichos-de-conta preferem ambientes escuros.

No caso do projecto "Popper, a tábua de Galton e a experiência da dupla fenda", as duas tábuas de Galton foram construídas com 5 divisões na base (todas com a mesma largura), pelo que, para cada esfera depositada numa dada divisão, mais 4 divisões estariam disponíveis - sendo por isso que, na experiência conduzida pelos alunos do Clube de Ciências, o número de graus de liberdade é de 4.

Popper, a tábua de Galton e a experiência da dupla fenda: introdução e objectivo do projecto

No início do ano lectivo, os alunos André Gonçalves, Daniel Domingues e Luís Miguel Gil (da turma 9.º/6.ª) aceitaram o desafio de levar por diante o projecto "Popper, a tábua de Galton e a experiência da dupla fenda", com o objectivo de responder a uma questão colocada por Sir Karl Popper (um dos mais importantes filósofos da Ciência do séc. XX) sobre a famosa experiência da dupla fenda feita com electrões (ou outras partículas submicroscópicas, como mostra o vídeo abaixo com moléculas de ftalocianina).

A ideia do projecto veio da leitura de um post, num fórum de física, onde se aborda a posição realista de Karl Popper sobre a experiência da dupla fenda, usando como analogia uma tábua de Galton (ver exemplo no vídeo abaixo), uma máquina simples construída por Sir Francis Galton para estudar a distribuição normal de probabilidades (uma das mais importantes em estatística).

 

As ideias de Popper, enunciadas no seu livro A Teoria dos Quanta e o Cisma na Física (de 1982), encontram-se resumidas na citação abaixo (adaptada):

Considere-se, p. ex., uma vulgar tábua de Galton, simétrica, construída de tal modo que se fizermos descer por ela algumas esferas, estão formarão uma curva normal de destribuição. Essa curva representará a distribuição de probabilidades para cada experiência individual com cada uma das esferas de se alcançar um certo local possível de repouso no fundo da tábua.

"Pontapeemos" agora a tábua, digamos, elevando ligeiramente o seu lado esquerdo. Deste modo, pontapeamos também as propensões - a distribuição de probabilidades -, uma vez que passará a ser ligeiramente mais provável que cada uma das esferas alcance um ponto do lado direito da parte de baixo da tábua. E a propensão devolverá o pontapé: produzirá uma curva de esferas com uma configuração diferente se deixarmos estas descer e acumular-se.

 Ou, em vez disso, retiremos um prego da tábua. Isto irá alterar a probabilidade para cada experiência individual com cada uma das esferas, quer a esfera se aproxime efectivamente de onde retirámos o prego, ou não. (O que tem alguma semelhança com a experiência da dupla fenda, ainda que aqui não tenhamos sobreposição "ondas electrónicas", uma vez que podemos perguntar: "como é que a esfera 'sabe' que se retirou um prego se ela nunca se aproxima desse local?". A resposta é que a esfera não "sabe"; mas a tábua no seu todo "sabe" e altera a distribuição de probabilidades, ou propensão, para cada esfera, facto que pode ser testado por testes estatísticos.)

O autor do referido post continua o raciocínio de Popper considerando que esses testes seriam uma excelente experiência para alunos do ensino médio (3.º ciclo do ensino básico e ensino secundário) realizarem, desafio esse que foi aceite pelos alunos do Clube de Ciências (organizados no grupo Os Poppers), resultando no seguinte objectivo de trabalho:

Realizar um teste estatístico simples (o teste do qui-quadrado) para verificar se a distribuição de esferas obtida para uma tábua de Galton sem um prego (que vai servir de análogo à experiência da dupla fenda) é significativamente diferente da distribuição de esferas obtida para uma tábua de Galton normal (que vai servir de análogo à experiência de difracção por uma única fenda), permitindo assim apoiar (ou não) as ideias de Popper sobre a experiência da dupla fenda. 

Participação na Exposição AMADORA EDUCA 2013 (31 de Maio)

Acompanhando a prof.ª Marta Albuquerque (coordenadora do Programa Eco-escolas), e no seguimento de não terem conseguido concluir o seu projecto científico, no dia 31 de Maio, os alunos do Clube de Ciências Denis Santos, Mamadu Baldé e Tomás Francisco (da turma 9.º/6.ª) ajudaram a dinamizar o stand do Agrupamento Escolar na Exposição AMADORA EDUCA 2013, desempenhando de forma muito positiva o papel de monitores das experiências dos vários Clubes/Projectos da escola levadas para a Exposição.

Abaixo apresentam-se várias fotografias a documentarem as actividades realizadas no stand do Agrupamento Escolar, com especial ênfase para a prestação dos alunos do Clube, sendo de referir que os  telefones de cordel construídos no Clube de Ciências, pelo grupo de alunos do 7.º ano Os Comunicadores, tiveram particular adesão por parte do público, especialmente dos mais novos.

1. A 'Ilha Mágica do Lido', local onde se realiza anualmente a Exposição AMADORA EDUCA.

2. Stand do Agrupamento Escolar (designado agora por Agrupamento Pioneiros da Aviação Portuguesa) decorado com o tema O Mar, da responsabilidade do 1.º ciclo.

3. Outra vista do stand do Agrupamento Escolar.

4. Banca do stand do Agrupamento com os vários trabalhos elaborados no Programa Eco-escolas, Clube de Ciências e Clube de Biologia da Escola Básica Roque Gameiro.

5. Pormenor da banca, evidenciando a participação do Clube de Ciências com os telefones de cordel construídos pelo grupo de alunos do 7.º ano Os Comunicadores.

6. Os alunos do Clube de Ciências, Denis Santos, Mamadu Baldé e Tomás Francisco, a prepararem um dos telefones de cordel para demonstração.

7. Alunos do 1.º ciclo a visitarem o stand do Agrupamento Escolar, e o aluno Mamadu Baldé com um dos telefones de cordel (em preparação para os alunos do 1.º ciclo).

8. Demonstração do funcionamento do telefone de cordel mostrado na fotografia anterior, pelo aluno Mamadu Baldé, com os alunos do 1.º ciclo.

9. Preparação da demonstração do funcionamento dum barco (protótipo) movido a energia solar, do Programa Eco-escolas, na pisicina do recinto.

10. Demonstração do funcionamento do protótipo da fotografia anterior.

11. Actividades desportivas disponíveis para o público mais jovem, realizadas durante o AMADORA EDUCA 2013.

12. Mais actividades lúdicas realizadas durante o AMADORA EDUCA 2013.



Visita de estudo ao Media Lab - Centro Educativo do Diário de Notícias (7 de Dezembro de 2012)

No final do 1.º período, os professores coordenadores do Programa Eco-escolas (Marta Albuquerque), do Clube de Ciências (Orlando R. Gonçalves) e do Clube de Biologia (José Madeira) organizaram uma visita de estudo ao Centro Eucativo do Diário de Notícias - Media Lab, com as turmas 9.º/5.ª e 9.º/7.ª, tendo os alunos do 9.º ano do Clube de Ciências participado também na visita. A visita de estudo contou ainda com a presença da prof.ª de Português da turma 9.º/5.ª, Ana Paula Capela.

A visita de estudo, além de dar a conhecer a história de 145 anos do DN - através de uma breve visita guiada ao edifício do jornal e de um curto filme visionado no auditório -, englobou também a oficina de escrita científica "Falando de Ciências", onde os alunos produziram pequenos trabalhos jornalísticos sobre questões actuais e que fossem do seu agrado, dentro dos temas Ciência, Tecnologia e Ambiente (daí a conjugação de esforços do Clube de Ciências, do Clube de Biologia e do Programa Eco-escolas). 

Esta oficina foi de particular interesse para os alunos do Clube de Ciências, uma vez que os trabalhos de projecto por si desenvolvidos no clube incluíram sempre uma vertente de comunicação dos mesmos (compreendendo um relatório, um póster científico e a defesa pública dos respectivos projectos), com vista à participação na 7.ª Mostra Nacional de Ciência.

As fotografias abaixo documentam a visita de estudo, incidindo sobretudo na participação dos alunos do Clube de Ciências (sendo também visível a presença dos professores coordenadores dos três Projectos/Clubes do Agrupamento Escolar):

Telefone de cordel: uma experiência clássica com ondas sonoras

Outro projecto realizado, no 2.º período, pelo grupo de alunos Os Comunicadores (Rúben Rocha, Luís Carlos e Rafael Anacleto (das turmas 7.º/8.ª e 7.º/6.ª, respectivamente) foi uma experiência (brincadeira) clássica de miúdos: a construção de um telefone de cordel... (ver o excerto abaixo do programa infantil Jornalinho de 1986, com o então coronel de artilharia do exército José Lúcio Ribeiro de Almeida):

Explicações mais detalhadas sobre a construção dum telefone de cordel e o modo como as ondas sonoras se propagam neste (fáceis de relacionar com a matéria de física do 8.º ano de escolaridade) podem ser encontrados aqui e aqui.

Mais informações e material didáctico interactivo sobre ondas, som e luz podem ser encontrados no excelente website Sounds Amazing da Universidade de Salford, para quem se sente mais à vontade com o inglês.

A fotografia abaixo mostra os alunos do Clube a testarem um dos dois 'telefones de cordel' construídos (um de corda e o outro com fio de algodão), de modo a determinarem qual deles era o melhor transmissor de som.

Depois de vários ensaios realizados por todos os alunos do 7.º ano do Clube de Ciências, determinou-se que o telefone com fio de algodão era o melhor transmissor de ondas sonoras, muito provavelmente por ser um meio mecânico mais homogéneo e de maior elasticidade que a corda, mais fácil por isso de ser esticado.

Ambos os 'telefones' fizeram parte das experiências apresentadas/realizadas durante o Laboratório Aberto de Físico-Química (a 3 de Maio) e no stand do Agrupamento Escolar durante a Exposição AMADORA EDUCA 2013 (de 29 de Maio a 2 de Junho).