De modo a manter tudo o mais simples possível, os alunos do Clube de Ciências aprenderam o teste do qui-quadrado a partir do livro Nuffield Science Calculations, dirigido a alunos ingleses dos 11-14 anos e 14-16 anos inscritos em cursos GCSE de Ciência.
O qui-quadrado é, então, uma variável estatística calculada a partir do somatório das diferenças entre os resultados observados, Oi, e os resultados esperados, Ei, de acordo com a seguinte fórmula:
onde i = 1, 2, ..., k é o n.º de divisões (ou classes ou 'caixas') pelas quais se distribuem os vários resultados.
Comparando o valor calculado com certos valores críticos (que dependem do nível de probabilidade e dos chamados 'graus de liberdade') é possível determinar quão bem os resultados observados se aproximam dos esperados. A tabela abaixo apresenta vários desses valores críticos, para diferentes níveis de probabilidade (em %) e graus de liberdade (g.l.):
O exercício seguinte, retirado do livro supracitado, pode mostrar como se aplica o teste do qui-quadrado e qual o significado dos 'graus de liberdade'.Considere-se uma experiência simples com 96 bichos-de-conta contidos numa caixa dividida em duas metades, estando a metade A às escuras e a metade B iluminada. Com todas as outras variáveis controladas, o n.º observado de bichos-de-conta em cada uma das metades foi:
Metade A (às escuras): 73 bichos-de-conta || Metade B (iluminada): 23 bichos-de-conta
RESOLUÇÃO:
Dados:
Oescuro = 73; Oiluminado = 23
Eescuro = 48; Eiluminado = 48 (admitindo que os bichos-de-conta se distribuíram aleatoriamente pelas duas metades da caixa)
Calculando o valor do qui-quadrado, obtém-se:
No caso do projecto "Popper, a tábua de Galton e a experiência da dupla fenda", as duas tábuas de Galton foram construídas com 5 divisões na base (todas com a mesma largura), pelo que, para cada esfera depositada numa dada divisão, mais 4 divisões estariam disponíveis - sendo por isso que, na experiência conduzida pelos alunos do Clube de Ciências, o número de graus de liberdade é de 4.
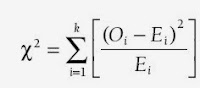


Sem comentários:
Enviar um comentário